Eins null eins null eins null – Wie Delphi intern tickt
Floats und der verwandte Currency
Fließkommazahlen sind oft das Herzstück unserer Berechnungen. Sie können viel größere Wertebereiche abdecken als Integers und doch haben auch sie ihre Schwächen. Das soll an einem weiteren Beispiel gezeigt werden.
begin writeln((1e20 + -1e20) + 3.14); writeln(1e20 + (-1e20 + 3.14)); readln; end.
(Die Zahl 1e20 ist übrigens nur eine Kurzform für die Fließkommazahl 1 * 1020.)
Was haben wir hier nun gemacht? Wir haben im Grunde ein und dieselbe Rechnung unterschiedlich aufgeschrieben. Die Addition ist mathematisch gesehen assoziativ. Das bedeutet, wir können klammern wie wir wollen. (a + b) + c = a + (b + c). Diese Regel haben wir angewendet. Wir erwarten also bei beiden Rechnungen das Ergebnis 3.14. Tatsächlich erhalten wir aber folgende Ausgabe:
3.1400000000000000E+0000
0.0000000000000000E+0000
Aufgrund der Kurzschreibweise ist dies identisch mit 3.14
0.0
Überlegen wir uns nun, was passiert ist. Im ersten Fall haben wir zunächst 1e20 – 1e20 gerechnet. Die Zahlen haben sich ausgelöscht und übrig blieb 0:0 + 3.14 übrig. Im zweiten Fall haben wir hingegen zuerst -1e20 + 3.14 gerechnet. Da auch Fließkommazahlen nur begrenzten Speicherplatz einnehmen, haben wir dummerweise den Genauigkeitsbereich durch die Addition verlassen. Bei der Addition müssen zunächst die Exponenten beider Zahlen aus technischen Gründen angeglichen werden. Genau hier ist der Fehler passiert. Das Phänomen mit der Genauigkeit kann uns auch nur bei Fließkommazahlen passieren. Bei sogenannten Festkommazahlen geht das nicht – ebenso wenig wie bei Integerzahlen.
Dennoch haben Fließkommazahlen einen unschätzbaren Vorteil gegenüber Festkommazahlen. Diese Zahlen sind so gebaut, dass sie in der Nähe der Null eine wesentlich höhere Genauigkeit besitzen. Der Grundgedanke ist dabei, eine Anzahl signifikanter Stellen (Mantisse) samt Vorzeichen zu speichern und zusätzlich um wie viel das (gedachte) Komma verschoben werden muss (Exponent). Dabei ist zu beachten, dass es sich hierbei um binäre Stellen handelt und auch sonst das Format komplizierter ist. Für Details siehe IEEE 754.
Um das Prinzip zu verdeutlichen nehmen wir mal vereinfachend an, es handele sich um dezimale Stellen. Dann würde beispielsweise für die Zahl 12354567890000 1,23456789 als Mantisse gespeichert mit der Information „Schiebe das Komma um 12 Stellen nach rechts“ oder mathematisch als Exponent +12. 1.23456789 * 1012 = +1234567890000. Für 0.000123456789 würde ebenfalls 1.23456789 als Mantisse gespeichert, als Exponent aber -4. 1.23456789 * 10-4 = 0.000123456789.
Da die Mantisse in ihrer Größe beschränkt ist, lassen sich so zwar sehr große, sowie sehr kleine Werte darstellen, aber nur mit der begrenzten Genauigkeit der Mantisse. Folgendes Bild zeigt, welchen Zahlenbereich ein fiktiver 5-Bit-Gleitkommadatentyp einnehmen kann. Wir sehen, dass die Abstände der darstellbaren Zahlen größer werden, je weiter wir uns von der Null entfernen.
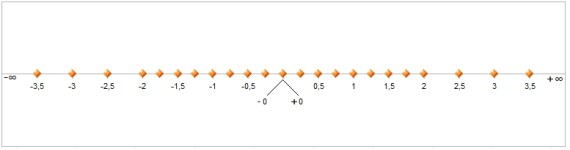
Die erwähnten Eigenschaften erzeugen neue Probleme. So trifft man zum Beispiel bei mathematischen Näherungsverfahren häufig auf das Problem, dass man das Verfahren abbrechen lassen möchte, sobald es genügend genau ist. Das folgende, etwas vereinfachte Beispiel, berechnet etwa mithilfe des sogenannten Newton-Verfahrens die Nullstelle der Funktion f: x -> x2 – 0.01, welche genau die Wurzel von 0.01 darstellt (Wurzel aus 0.01 = 0.1). Es soll abbrechen, sobald die Nullstelle erreicht ist.
function f(x: extended): extended;
begin
// Berechne den Funktionswert
result := x * x - 0.01;
end;
function fdiff(x: extended): extended;
begin
// Berechne den Funktionswert des Differentials.
result := 2 * x;
end;
function newton(xStart: extended): extended;
begin
if (f(xStart)=0) then
begin
// Wir sind fertig. Liefere das Ergebnis zurück .
result := xStart;
end
else
begin
// Genauigkeit noch nicht erreicht.
// Rufe das Verfahren erneut auf.
result := newton (xstart - f(xStart) / fdiff(xStart));
end;
end;
begin
// Wende das Newtonverfahren mit Startwert x=1 an.
writeln(newton(1));
readln;
end.
Die eigentliche Überprüfung findet mit if (f(xStart) = 0) statt. Das Problem ist jedoch, dass die Nullstelle irgendwann soweit angenähert ist, dass der Datentyp nicht noch mehr Nachkommastellen speichern kann. Setzt man die Nullstelle dann in der Funktion ein, erhält man einenWert, der sehr nahe an der Null liegt – aber eben noch nicht Null ist. Das Verfahren terminiert nicht. Ein derartiger Vergleich ist also nutzlos. Besser ist es da, einen gewissen Toleranzbereich mitzuliefern. Wird dieses Limit unterschritten, ist die Nullstelle genau genug.
function newton(xStart: extended ; epsilon: extended): extended;
begin
if (abs(f(xStart)) < epsilon) then
result := xStart
else
result := newton(xstart - f(xStart) / fdiff(xStart), epsilon);
end;
Wir bilden also zunächst den Betrag des berechneten Wertes (dieser könnte ja auch negativ sein) und schauen dann, ob wir in unserem gewünschten Genauigkeitsbereich sind. Wenn ja, liefern wir das Ergebnis zurück. Ähnlich funktioniert es übrigens beim Vergleichen von zwei Fließkommazahlen. Ein direkter Vergleich per = ist riskant, denn eine kleine Ungenauigkeit kann schon dafür sorgen, dass der gewünschte Fall nicht eintritt. Ein solches Beispiel hatten wir schon zu Anfang des Kapitels gesehen, als ein und dieselbe Rechnung unterschiedliche Ergebnisse geliefert hat. Wir können übrigens auch die bereits eingebauten Funktionen CompareValue oder SameValue von Delphi nutzen. Diesen kann man ebenfalls eine Differenz mitliefern, innerhalb welcher zwei Gleitkommazahlen als identisch betrachtet werden.
Nun soll auch der Currency-Datentyp noch erwähnt werden. Er ist der bereits vorher angesprochene Festkommazahlendatentyp. Er wurde mit dem Ziel entworfen, die Rundungsfehler im finanzmathematischen Bereich zu minimieren. Im Gegensatz zu Fließkommazahlen wird er nicht über die sogenannte FPU (Floating-Point-Unit) berechnet, sondern stattdessen intern wie ein Integer gehandhabt. Das vermeidet die offensichtlichen Schwächen mit den Genauigkeitsunterschieden, reduziert jedoch die Anzahl der Nachkommastellen auf genau vier Stellen. Wenn man ihn verwendet, sollte man allerdings aus naheliegenden Gründen vermeiden ihn mit anderen Datentypen zu mischen.
Wir merken also: Die reellen Zahlen im Computer entsprechen nicht den mathematischen reellen Zahlen.
Zu guter Letzt gibt es auch zu den Fließkommazahlen und dem Currency-Datentyp noch eine Tabelle (Hierbei bezeichnen die signifikanten Stellen die Anzahl der angegebenen Ziffern einer Zahl ohne die führenden Nullen):
| Name | Größe (in Bit) | Signifikante Stellen | Wertebereich |
|---|---|---|---|
| Single | 32 | 7-8 | 1.5*10-45 … 3.4*1038 |
| Double | 64 | 15-16 | 5.0*10-324 … 1.7*10308 |
| Extended | 80 | 10-20 | 3.6*10-4951…1.1*104932 |
| Currency | 64 | 10-20 | -922337203685477.5808… 922337203685477.5807 |
| Name | Größe (in Bit) | Signifikante Stellen | Wertebereich |
|---|---|---|---|
| Real | 64 | 15-16 | 5.0*10-324 … 1.7*10308 |
