Rekursive Algorithmen
Türme von Hanoi
So, jetzt haben wir gespielt. Nun geht es wieder an die Arbeit.
Rufe Dir doch jetzt mal (aus der Datei tutrkalg.exe) die Datei Loesung.exe auf. Zu dieser Datei gibt es keinen Quelltext, Du sollst Dir einfach einmal Bestätigung für Deine gut gewählten und überlegten Züge im Spiel holen.
So, jetzt hast Du gesehen, wie gut Du warst. Und nun kannst Du Dir überlegen, wie Du den Algorithmus für so einen Spielablauf programmieren willst.
Im Schritt Modularisierung haben wir uns überlegt, wie wir an eine größere Programmieraufgabe herangehen könnten. Lies Dir diesen Schritt am besten noch einmal durch.
Die Bottom-Up-Methode scheint uns nicht viel zu bringen. Wir sehen erst einmal das Riesenproblem vor uns und können nicht ohne weiteres von kleinen Teillösungen auf größere Strukturen kommen.
Also wollen wir es mit der Top-Down-Methode versuchen.
Hier finden wir auch schon einen Ansatz zu unserem Vorhaben, Probleme rekursiv zu lösen. Das Bild „Teile und Herrsche“ (siehe weiter vorn) macht es uns optisch deutlich.
Aber jetzt wird es endlich erst einmal Zeit, die Frage zu stellen: Was ist das eigentlich mit dem rekursiven Denken? Was ist das mit den rekursiven Algorithmen??
Lies Dir jetzt am besten erst einmal die Information in der Datei Legende.hlp (in den Beispieldateien) durch. Durch Anklicken rufst Du sie auf.
Die „Türme von Hanoi“ sind ein ausgezeichnetes Beispiel für das, was man rekursives Denken nennt. Frei vom Druck einer Weltuntergangsstimmung können wir es uns leisten, mit ganz geringen Scheibenzahlen zu beginnen.
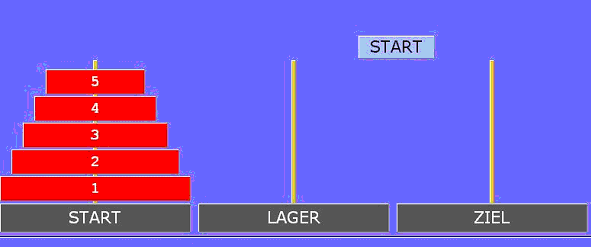
Um keine Scheibe von Nadel START nach Nadel ZIEL zu bringen, ist natürlich keine Umlegung nötig, für eine Scheibe offenbar genau eine Umlegung. Bei zwei Scheiben deponierst Du zuerst die kleine Scheibe auf der Nadel LAGER, bringst dann die größere Scheibe auf Nadel ZIEL und kannst mit dem dritten Zug den Turmbau auf ZIEL mit dem Hinüberlegen der kleineren Scheibe abschließen.
Nehmen wir an, Du weißt, wie n Scheiben umzulegen sind. Wie geht es dann mit n+1 Scheiben weiter? Genau, wie eben beschrieben. Du baust den Turm aus den n Scheiben im Zwischenlager (LAGER) statt im ZIEL auf, was ich als bekannt unterstelle, um dann die unterste (n+1)-Scheibe auf der Nadel ZIEL abzulegen. Jetzt kannst Du mühelos den zwischengelagerten Turm aus n Scheiben auf die größte Scheibe versetzen. – Damit ist das Grundprinzip klar.
Ratsam ist es, jetzt noch einmal zum Spiel mit den Würfeln zurückzukehren. Lass Dir das eben Gesagte langsam „auf der Zunge zergehen“ und spiele es mit den Würfeln nach (aber nicht auf der Zunge).
Eine praktikable Regel ist folgende:
Die drei Stangen (Nadeln) werden in Dreiecksform angeordnet. Es müssen nicht unbedingt „Diamantnadeln“ sein (wie in der Legende).
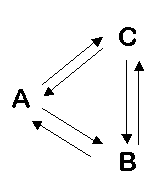
Du legst die kleinste Scheibe von Nadel A auf Nadel B (gerade Zahl von Scheiben) oder auf Nadel C (ungerade Zahl von Scheiben) und bewegst diese Scheibe nur in dem hierdurch festgelegten Umlaufsinn (ABCAB … bzw. ACBAC …) Die nächste Scheibe legst Du so, dass die kleinste Scheibe nicht berührt wird, und behältst den Umlaufsinn bei. Wenn Du die Scheiben von oben nach unten durchnummerierst (anders wie im obigen Bild), so wandern die Scheiben mit ungerader Nummer wie die kleinste Scheibe über die Nadeln, während sich die restlichen Scheiben entgegengesetzt bewegen.
Wie viele Umlegungen werden für die Scheiben benötigt?
Um n Scheiben von A nach C zu bringen, sind 2 hoch n – 1 Umlegungen nötig, für acht Scheiben sind das immerhin schon 255 Umlegungen und für 64 Scheiben (die Zahl in der Legende) ist das eine nicht vorstellbare 20-stellige Zahl. Da haben die Priester im Tempel von Benares aber noch zu tun!
Um es genauer zu sagen: Für 64 Scheiben wären also 2 hoch 64 – 1 Umsetzungen nötig. Dies sind ungefähr 18,45 Trillionen (18,45*10 hoch 18) Umsetzungen. Wenn man für eine Umsetzung 20 Sekunden rechnet, so würden bis zur Lösung der Aufgabe etwa 11,7 Billionen Jahre vergehen.
Übrigens: Wer sich im Rechnen üben will, kann sich ja solche Fragen wie „Wie sieht die Verteilung von n Scheiben nach dem p-ten Zug aus?“ oder „Wie oft und wann wird beim Umsetzen eines Turmes von n Scheiben die k-te Scheibe bewegt?“ vornehmen. Wenn Du Freude an solchen Fragen hast, dann viel Spaß. Wenn nicht, geht die Welt auch nicht unter (die Priester sind noch nicht so weit).
